Ground Control Points (GCP) utilised in the production of a Digital Elevation Model (DEM) can also play part of a post processing technique to indicate how accurate the surface model is. Even when GCP aren’t used in model creation, they can be used to assess the accuracy of a DEM through their introduction into a survey area after modelling.

The Root Mean Squared Error (RMSE) is used as a way of communicating a surface models accuracy. It is determined as a function of the elevation difference between a number of GCP’s and the model at corresponding locations.

RMSE is represented by the following formula:

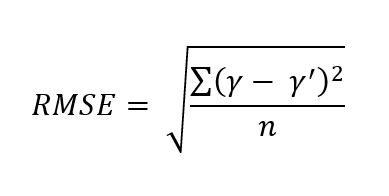
For those not mathematically inclined, don’t be scared off (or by the remaining remarks). RMSE is calculated from the square root of the Mean Square Error (MSE).  MSE is calculated as the average of the summed squared differences between the modelled elevation at each GCP location and the surveyed value.

The RMSE value can be calculated within Excel, however is typically provided as part of a models processing report when GCP have been included in the models creation.

The following table (obtained from an excerpt of a processing report) could also be prepared in Excel, shows a working calculation for determination of RMSE by using the function:

= SQRT(SUMSQ(F2:F16)/COUNT(F2:F16)):

	A	B	C	D	E	F
1	Point name	East	North	GCP Elevation (m)	DEM Elevation (m)	Diff.(D-E)
2	ac754588d1	X4321.360	X5364.292	110.119	110.094	0.025
3	ac2b3042bf	X3821.179	X5642.205	120.385	120.363	0.022
4	ac52bf45d2	X4061.849	X5678.942	109.895	109.909	-0.014
5	ac68ec841d	X4069.613	X5466.665	101.727	101.719	0.008
6	ac84d610b2	X4098.876	X5377.983	102.445	102.454	-0.009
7	ac7a468b34	X4029.881	X5238.401	126.685	126.684	0.001
8	aca8db056a	X3887.846	X5096.814	144.677	144.671	0.006
9	acf4c7d218	X3896.366	X4965.553	161.931	161.933	-0.002
10	ac03171cb5	X4208.823	X5104.645	107.022	107.030	-0.008
11	acaea33855	X4256.865	X4737.683	94.932	94.945	-0.013
12	acea2c48e8	X4473.320	X5198.068	117.700	117.693	0.007
13	acdec6e604	X4655.533	X4828.529	147.675	147.680	-0.005
14	acc0b6259f	X3876.210	X4731.457	189.267	189.283	-0.016
15	acb570697d	X3915.187	X5526.109	109.130	108.442	0.688
16	ac49a92b1b	X4277.829	X4606.666	181.602	181.587	0.015

The difference between the model at each corresponding GCP location is first calculated, by subtracting column E from D and reporting the result in column F. The RMSE is then calculated using the supplied formula producing a value of 0.178 m or 17.8 cm. This error is higher than typically expected and would not be considered acceptable for a survey grade surface model.

Reviewing the tabled result’s we see that one GCP, acb570697d (row 15), has a difference between the surveyed GCP elevation and the modelled DEM of close to 69 cm. This location requires further investigation in the 3D graphical environment.

Examining this GCP location against the terrain model, (the later draped with the orthophoto) we can identify that the model is impacted by post process filtering.

An ‘Equipment’ filtering algorithm applied during processing, which is designed to remove man made objects from the model, has flattened a block upon which the GCP pad was affixed.

Removing GCP acb570697d from the RMSE calculation, and only relying on 14/15 sites reports a revised RMSE value of 0.013 m or 1.3 cm. This is an acceptable result for the model, enabling it to be considered survey grade in non vegetated areas.

The key learning for GCP placement and obtaining an initial valid RMSE value is to avoid having GCP located on top of blocks or other elevated structures. The difference between the elevation in the model and that of the corresponding GCP can be significant, particularly if filtering is carried out to remove man made features from the model. 

Increased error between the DEM and GCP affixed to blocks can also be the result of the gridded surface representing the DEM being unable to replicate the sharp shape change in the concrete blocks dimensions.

To determine RMSE correctly, we recommend that all GCP should be as close as possible to ground level. However, we note that site conditions at times favour using elevated positions to increase longevity of GCP.  Spend time looking at alternative locations to avoid the use of blocks where possible. Consider the removal of filtering algorithms as a post process. However, in removing filters, this may result in other issues, like then having to manually post edit out equipment positioned near to features you are estimating volumes on.

Always critically evaluate process reports to understand the true meaning of reported RMSE when assessing survey accuracy.  Avoid the creation of false errors or distortion of the error by keeping GCP on the ground where they belong.

Furthermore, remember that photogrammetric models over heavily vegetated areas are never accurate. Models in these area represent the canopy of the vegetation and not bare earth.  Employ alternative capture techniques like LiDAR to increase the accuracy of the model and determine a bare earth position when dealing with vegetation cover.

---